Calculates Person correlation coefficients between X and Y representing two samples/variables with X and Y Values being treated as observables. 

If X and Y are two matrices, the rouitine calculates Pearson correlation coefficients r_x,y between X and Y matrix. The algorithm assumes X and Y are two samples (variables) and all X are are treated as it's observables (same goes for Y). 

Note The correlation is defined only if both of the standard deviations are finite and both of them are nonzero. 

Correlation coefficient 

The correlation coefficient rho between two random variables is defined by the following equation: 

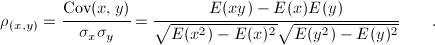
where x,y are two variables, Cov covariance betwen x and y, sigma(s) their expected standard deviations and E-s their expected values. If the variables are independent then the correlation is 0, but the converse is not true because the correlation coefficient detects only linear dependencies between two variables. 

Sample correlation coefficients. 

If we have a series of n measurements of X and Y, then the Pearson product-moment correlation coefficient can be used to estimate the correlation of X and Y. The Pearson coefficient is also known as the "sample correlation coefficient". The Pearson correlation coefficient is then the best estimate of the correlation of X and Y .

Calculate correlation coefficients from Data1 and Data2 representing two variables.

CorrCoef Method